79.单词搜索

一、题目

给定一个m x n二维字符网格board和一个字符串单词word。如果word存在于网格中，返回true；否则，返回false。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例一：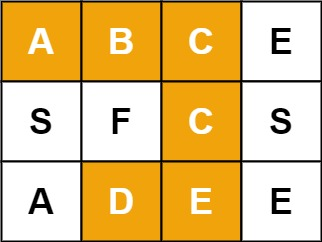

输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCCED”
输出：true

示例二：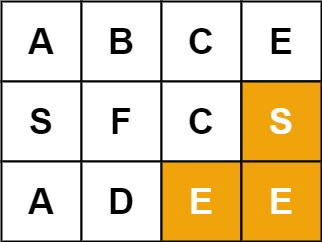

输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “SEE”
输出：true

示例三：

输入：board = [[“A”,”B”,”C”,”E”],[“S”,”F”,”C”,”S”],[“A”,”D”,”E”,”E”]], word = “ABCB”
输出：false

提示：

m == board.length
n = board[i].length
1 <= m, n <= 6
1 <= word.length <= 15
board和word仅由大小写英文字母组成

进阶：你可以使用搜索剪枝的技术来优化解决方案，使其在 board 更大的情况下可以更快解决问题？

二、相关链接

题目链接：https://leetcode-cn.com/problems/word-search/
参考题解：https://leetcode-cn.com/problems/word-search/solution/su-kan-dfsjian-dan-yi-dong-by-rain-ru-xnwe/

三、解题思路

解法：回溯算法
思路：理解为三叉树即可，然后参考全排列

四、代码

public class WordSearch {
    
    public boolean exist(char[][] board, String word) {
        //这种有结束条件的一般都要想到回溯
        char[] words = new char[word.length()];

        //找到第一个字符
        char first = word.charAt(0);
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[0].length; j++) {
                //找到起点
                if (board[i][j] == first) {
                    //还是得设置一个boolean数组
                    boolean[][] isUsed = new boolean[board.length][board[0].length];
                    boolean isExist = this.backtrack(board, words, isUsed, i, j, 0, word);
                    //只要有一条路径符合即可
                    if (isExist) {
                        return true;
                    }
                }
            }
        }
        return false;
    }

    //words存放路径
    //board记录走过的(设置0即可)
    //word存放需要走的单词

    /**
     * 回溯算法
     * @param board 二维字符网络(条件给的，不变)
     * @param words 路径
     * @param isUsed 网络字符使用情况(路径走过置为true)
     * @param x
     * @param y
     * @param wordsSize
     * @param word
     * @return
     */
    public boolean backtrack(char[][] board, char[] words, boolean[][] isUsed, int x, int y, int wordsSize, String word) {
        //判断是否在便捷了
        if (x < 0 || x > isUsed.length - 1 || y < 0 || y > isUsed[0].length - 1) {
            return false;
        }

        //使用过也返回false
        if (isUsed[x][y]) {
            return false;
        }


        //判断是否可以连上
        if (board[x][y] != word.charAt(wordsSize)) {
            return false;
        } else {
            words[wordsSize] = board[x][y];
            wordsSize++;
            isUsed[x][y] = true;

            if (wordsSize == word.length()) {
                return true;
            }
        }


        //前后左右看
        boolean left = this.backtrack(board, words, isUsed, x - 1, y, wordsSize, word);
        boolean right = this.backtrack(board, words, isUsed, x + 1, y, wordsSize, word);
        boolean up = this.backtrack(board, words, isUsed, x, y - 1, wordsSize, word);
        boolean down = this.backtrack(board, words, isUsed, x, y + 1, wordsSize, word);

        //回溯算法关键，需要往回回滚数据
        isUsed[x][y] = false;

        //只要有一个有true即可
        return left || right || up || down;
    }

    /**
     * 输入：board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
     输出：true
     * @param args
     */
    public static void main(String[] args) {
        char[][] board = new char[][]{{'A', 'B', 'C', 'E'}, {'S', 'F', 'C', 'S'}, {'A', 'D', 'E', 'E'}};
        String word = "ABCCED";
        System.out.println(new WordSearch().exist(board, word));
    }
}